关于频率分辨率的2种解释

解释一：

频率分辨率可以理解为在使用DFT时，在频率轴上的所能得到的最小频率间隔

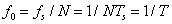
其中N为采样点数，fs为采样频率，Ts为采样间隔。所以NTs就是采样前模拟信号的时间长度T，信号长度越长，频率分辨率越好。

是不是采样点数越多，频率分辨力提高了呢？其实不是的，因为一段数据拿来就确定了时间T，注意：f0=1/T，而T=NTs，增加N必然减小Ts，因此，增加N时f0是不变的。只有增加点数的同时导致增加了数据长度T才能使分辨率越好。

还有容易搞混的一点，我们在做DFT时，常常在有效数据后面补零达到对频谱做某种改善的目的，我们常常认为这是增加了N，从而使频率分辨率变好了，其实不是这样的，补零并没有增加有效数据的长度，仍然为T。

但是补零其实有其他好处：

• 使数据N为2的整次幂，便于使用FFT。
• 补零后，其实是对DFT结果做了插值，克服“栅栏”效应，使谱外观平滑化。我把“栅栏”效应形象理解为，就像站在栅栏旁边透过栅栏看外面风景，肯定有被栅栏挡住比较多风景，此时就可能漏掉较大频域分量，但是补零以后，相当于你站远了，改变了栅栏密度，风景就看的越来越清楚了。
• 由于对时域数据的截短必然造成频谱泄露，因此在频谱中可能出现难以辨认的谱峰，补零在一定程度上能消除这种现象。

那么选择DFT时N参数要注意：

• 由采样定理：fs>=2fh，
• 频率分辨率：f0=fs/N，所以一般情况给定了fh和f0时也就限制了N范围：N>=fs/f0。

解释二：

频率分辨率也可以理解为某一个算法（比如功率谱估计方法），将原信号中的两个靠得很近的谱峰依然能保持分开的能力。这是用来比较和检验不同算法性能好坏的指标。在信号系统中我们知道，宽度为N的矩形脉冲，它的频域图形为sinc函数，两个一阶零点之间的宽度为4π/N。由于时域信号的截短相当于时域信号乘了一个矩形窗函数，那么该信号的频域就等同卷积了一个sinc函数，也就是频域受到sinc函数的调制了，根据卷积的性质，因此两个信号圆周频率之差W0必须大于4π/N。从这里可以知道，如果增加数据点数N，即增加数据长度，也可以使频率分辨率变好，这一点与第一种解释是一样的。同时，考虑到窗函数截短数据的影响存在，当然窗函数的特性也要考虑，在频率做卷积，如果窗函数的频谱是个冲击函数最好了，那不就是相当于没截断吗？可是那不可能的。

我们考虑窗函数主要是以下几点：

• 主瓣宽度B最小（相当于矩形窗时的4π/N，频域两个过零点间的宽度）。
• 最大边瓣峰值A最小（这样旁瓣泄露小，一些高频分量损失少了）。
• 边瓣谱峰渐近衰减速度D最大（同样是减少旁瓣泄露）。

在此，总结几种很常用的窗函数的优缺点：

• 矩形窗：B=4π/NA=-13dB D=-6dB/oct
• 三角窗：B=8π/NA=-27dB D=-12dB/oct
• 汉宁窗：B=8π/NA=-32dB D=-18dB/oct
• 海明窗：B=8π/NA=-43dB D=-6dB/oct
• 布莱克曼窗：B=12π/NA=-58dB D=-18dB/oct

可以看出，矩形窗有最窄的主瓣，但是旁瓣泄露严重。汉宁窗和海明窗虽主瓣较宽，但是旁瓣泄露少，是常选用的窗函数。

采样周期与频率分辨率

fs/N常称作为频率分辨率，它实际是作FFT时谱图中的两条相邻谱线之间的频率间隔，也有称作步长。单位是Hz、Khz等。频率分辨率实际有二重含义，在这里只是其中一种。

1/fs的单位的s、ms、us或分、时…年等。1/fs代表采样周期，是时间域上两个相邻离散数据之间的时间差。因此fs/N用在频率域，只在DFT以后的谱图中使用；而1/fs用时间域，只要数据经采样，离散化后任何其它的应用中都可使用。例如有的数字滤波器中就用到。

其中Δf是频率采样间隔，同时也是频率分辨率的重要指标，如果这个值越小，则频率分辨率越高。

1/fs往往用在求时间序列上，如 (0:N-1)*1/fs等等，如果这个不好理解，可以把前面的公式求倒数，这就清楚多了。

采样定理

采样过程所应遵循的规律，又称取样定理、抽样定理。采样定理说明采样频率与信号频谱之间的关系，是连续信号离散化的基本依据。采样定理是1928年由美国电信工程师H.奈奎斯特首先提出来的，因此称为奈奎斯特采样定理。1933年由苏联工程师科捷利尼科夫首次用公式严格地表述这一定理，因此在苏联文献中称为科捷利尼科夫采样定理。1948年信息论的创始人C.E.香农对这一定理加以明确地说明并正式作为定理引用，因此在许多文献中又称为香农采样定理。采样定理有许多表述形式，但最基本的表述方式是时域采样定理和频域采样定理。采样定理在数字式遥测系统、时分制遥测系统、信息处理、数字通信和采样控制理论等领域得到广泛的应用。

时域采样定理

频带为F的连续信号f(t)可用一系列离散的采样值f(t1)，f(t1±Δt)，f(t1±2Δt)，…来表示，只要这些采样点的时间间隔Δt≤1/2F，便可根据各采样值完全恢复原来的信号f(t)。

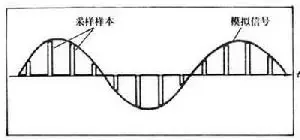
模拟信号采样示意图

时域采样定理的另一种表述方式是：当时间信号函数f(t)的最高频率分量为fM时，f(t)的值可由一系列采样间隔小于或等于1/2fM的采样值来确定，即采样点的重复频率f≥2fM。时域采样定理是采样误差理论、随机变量采样理论和多变量采样理论的基础。

频域采样定理

对于时间上受限制的连续信号f(t)（即当│t│>T时，f(t)=0。这里T=T2-T1是信号的持续时间），若其频谱为F(ω)，则可在频域上用一系列离散的采样值用下式表示

只要这些采样点的频率间隔

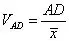
分析频率、采样点数、谱线数的设置要点

最高分析频率，Fm指需要分析的最高频率，也是经过抗混滤波后的信号最高频率。根据采样定理，Fm与采样频率Fs之间的关系一般为：

而最高分析频率的选取，决定于设备转速和预期所要判定的故障性质。

采样点数N与谱线数M有如下的关系：

N=2.56M，其中谱线数M与频率分辨率ΔF及最高分析频率Fm有如下的关系：

即：

所以：

采样点数的多少与要求多大的频率分辨率有关。例如：机器转速3000r/min=50Hz，如果要分析的故障频率估计在8倍频以下，要求谱图上频率分辨率ΔF=1Hz，则采样频率和采样点数设置为：

• 最高分析频率：Fm=8·50Hz=400Hz；
• 采样频率：Fs=2.56·Fm=2.56 ·400Hz=1024Hz；
• 采样点数：N=2.56·（Fm/ΔF）=2.56·（400Hz/1Hz）=1024=210；
• 谱线数：M=N/2.56=1024/2.56=400条。