上次计算矩阵都不知道是什么时候了，有亲戚在国外读书，最近时不时会问我一些高等数学的知识，说不会吧，怎么说咱也是数学系毕业，张不开这嘴，要说会吧，其实也忘得差不多了。
教解析几何的老师曾说过，“学过的知识，经过了忘记，还能保存在记忆中才是你自己的”，好吧，那就看看还记得多少高等数学的知识。
题目如下，直接上图：
刚才说过，这个亲戚是在国外读书，题目也是英文，在不使用翻译工具的情况大概能读懂意思。
翻译如下：下面哪个k值可以使得上面矩阵B可逆。题目中也给出了什么叫可逆。
对矩阵可逆最后的印象是满足两个条件：
第一：这个矩阵是方阵，即是n*n，n行n列 。
第二： 这个矩阵的行列式不为0。
说实话，我都不记得3*3矩阵的行列式的计算公式了，仅还记得矩阵的行或列进行线性变换后，不影响行列式的值，那我们就可以通过线性变换把这个矩阵B变成上三角或下三角形式，这样行列式的值就容易计算了，即对角线元素的乘积。废话不多说，解题过程如下。
行列式产生于解线性方程组，行列式的计算是一个重要的问题.计算行列式的几种常用方法：利用行列式的定义直接计算、化为三角形法、降阶法、利用范德蒙德行列式法、利用拉普拉斯定理法降阶法、递推法等.
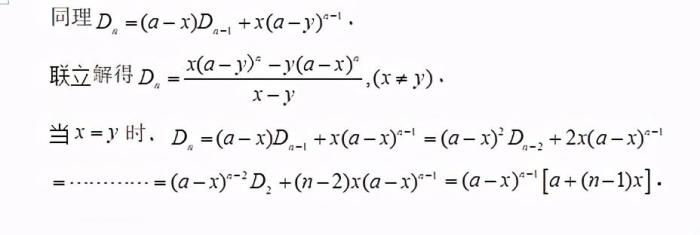
支付宝扫一扫
微信扫一扫
